By Noxxxx from https://www.noxxxx.com/?post_type=post&p=1003
欢迎分享与聚合,尊重版权,可以联系授权
JavaScript 中数字是如何表示的
JavaScript 中的所有数字都是浮点数,使用 64 位二进制来表示,也叫做双精度浮点型,这种方式出自于 IEEE-754 标准。

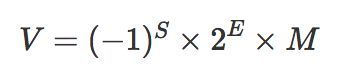
公式解读
- S (Sign/1bit):符号部分,当 S=0,V 为正数;当 S=1,V 为负数。
- E (Exponent/8bits):指数部分。E 是一个无符号整数,因为长度是11位,取值范围是 0~2047。但是科学计数法中的指数是可以为负数的,所以人们约定减去一个中间数 1023,
[0,1022]表示为负,[1024,2047]表示为正 - M (Mantissa/23bits):表示有效数字,大于等于1,小于2。第一位 1 可以被舍去,只保留小数部分节省一位有效数字。
指数 E 还分为三种情况:
- E 不全为 0 或不全为 1。这时,浮点数就采用上面的规则表示,即指数 E 的计算值减去 127(或 1023 ),得到真实值,再将有效数字 M 前加上第一位的 1。
- E 全为 0。这时,浮点数的指数 E 等于 1-127(或者 1-1023 ),有效数字 M 不再加上第一位的 1,而是还原为 0.xxxxxx 的小数。这样做是为了表示 ± 0,以及接近于 0 的很小的数字。
- E 全为 1。这时,如果有效数字 M 全为 0,表示 ± 无穷大(正负取决于符号位s);如果有效数字 M 不全为 0,表示这个数不是一个数(NaN)。
2^E 代表什么:
上面的公式其实是科学计数法的表示方式,十进制中我们如果想要对小数点进行前移或后移,就是 (一个数 ✖️ 10^1) 表示小数点往后移一位,同样的在二进制中就是采用(一个二进制数 ✖️ 2^1)表示二进制表达的数字的小数点往后移一位。
IEEE 754 中规定:
对于 32 位的浮点数,最高的 1 位是符号位 S,接着的 8 位是指数 E,剩下的 23 位为有效数字 M;
对于 64 位的浮点数,最高的 1 位是符号位 S,接着的11位是指数 E,剩下的 52 位为有效数字 M。
0.1 + 0.3 !== 0.3
> 0.1 + 0.2
0.30000000000000004
0.1 和 0.2 转换成 2 进制
> (0.1).toString(2)
"0.0001100110011001100110011001100110011001100110011001101"
> (0.2).toString(2)
"0.001100110011001100110011001100110011001100110011001101"
// 0.1 + 0.2
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111
// 转成十进制正好是 0.30000000000000004
误差怎么来的?
由于 IEEE 754 的规定,用 64 位二进制来表示数字,如果我们手动去转换一下十进制的 0.1 到二进制,
// 0.1 -> 二进制表示
0001100110011001100110011001100110011001100110011001100(1100一直循环下去)
// 按照 IEEE 754 的规定,套公式,用科学计数法表示成 1.xxx * 2^-x 的方式,所以小数点往后移
1.100110011001100110011001100110011001100110011001100(1100一直循环下去)
// 小数点后的这部分是尾数,尾数长度 == 小数值精度 == 尾数所代表二进制的个数越多就越精确,而按照规定我们只有 52 位,超出的能进位就进位,所以最终表示为
1.100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 11010
这么一来,像 0.1 这样的数值就不是精确的,不精确的两个数值做运算,结果显而易见,这里有个网站可以将二进制的展示方式表现出来。

另外根据二进制转换为十进制的公式,如果你使用 Math.pow() 去计算的话,会发现结果就是 0.1,然而我经过手算(0.1.toString(2) 转换为十进制)后实际结果是和0.1.toPrecision(x) 相近的,因为我是按照实际保留的尾数进行计算的,精度上没有 0.1.toPrecision(x) 高,但是在相同精度内结果是一致。
> Math.pow(2,-4) +
Math.pow(2,-5) +
Math.pow(2,-8) +
Math.pow(2,-9) +
Math.pow(2,-12) +
Math.pow(2,-13) +
Math.pow(2,-16) +
Math.pow(2,-17) +
Math.pow(2,-20) +
Math.pow(2,-21) +
Math.pow(2,-24) +
Math.pow(2,-25) +
Math.pow(2,-28) +
Math.pow(2,-29) +
Math.pow(2,-32) +
Math.pow(2,-33) +
Math.pow(2,-36) +
Math.pow(2,-37) +
Math.pow(2,-40) +
Math.pow(2,-41) +
Math.pow(2,-44) +
Math.pow(2,-45) +
Math.pow(2,-48) +
Math.pow(2,-49) +
Math.pow(2,-52) +
Math.pow(2,-53) +
Math.pow(2,-55)
0.1
0.1.toPrecision(29)
"0.10000000000000000555111512313"
相关链接:
JavaScript 浮点数陷阱及解法
JavaScript 里最大的安全的整数为什么是2的53次方减一?
IEEE 754 标准
采用 IEEE 754 的编程语言
IEEE 754 二进制可视化展示
十进制转二进制公式